【ITパスポート】2進数・10進数・16進数の表記法と基数変換を分かりやすく解説

ITパスポート試験では、情報処理の基本的な知識として「基数変換」がよく出題されます。
2進数・10進数・16進数といった進数表記は、コンピューターの仕組みを理解するうえで欠かせません。
本記事では、ITパスポート試験対策として、進数の表記法と基数変換の方法をわかりやすく解説します。「基数変換」に自信をつけたい方は、ぜひ参考にしてください。

2進数・10進数・16進数
1. 進数の表記法
2. 基数
基数変換

2進数・10進数・16進数

進数の表記法

まずは「2進数・10進数・16進数」、それぞれの表記法を見ていきましょう。

2進数・10進数・16進数の表記法

2進数：値が2になるときに桁が1つ上がる表記法
コンピュータの世界では基本的に、この2進数ですべての処理が行われています。

10進数：値が10になるときに桁が1つ上がる表記法
日常的に使っている表記法です。

16進数：値が16になるときに桁が1つ上がる表記法
10～15までの値を、AからFまでのアルファベットで表しています。

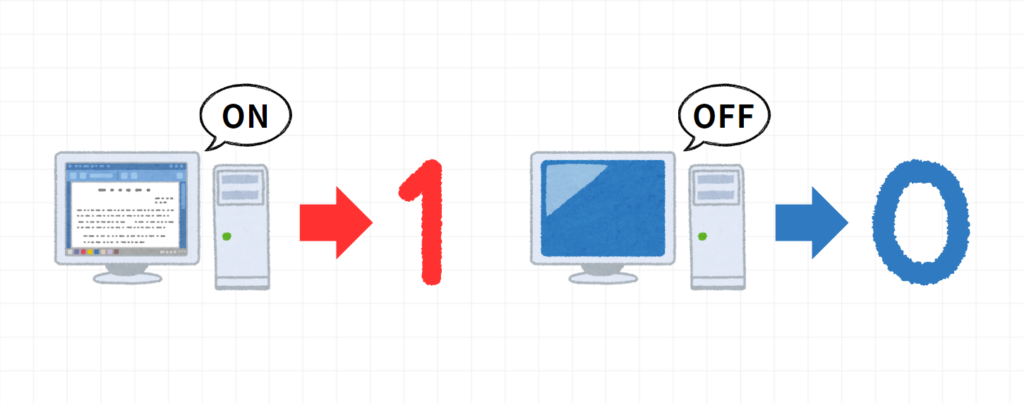
コンピュータの世界では基本的に、2進数（0と1）ですべての処理が行われています。電圧が低い状態を「0」、電圧が高い状態を「1」として情報を扱うためです。

ただし、コンピュータ内部では常に2進数が使われますが、私たちがデータを見たり管理したりする際には、10進数や16進数といった他の進数表記に変換して表示されることがあります。
例えば、メモリのアドレスやカラーコードの表示では16進数がよく使われます。

このように、2進数はコンピュータの基本的な仕組みを理解するために欠かせない重要な概念であることが分かると思います。

基数

「基数変換」の解説に行く前に、「基数」について簡単に解説します。
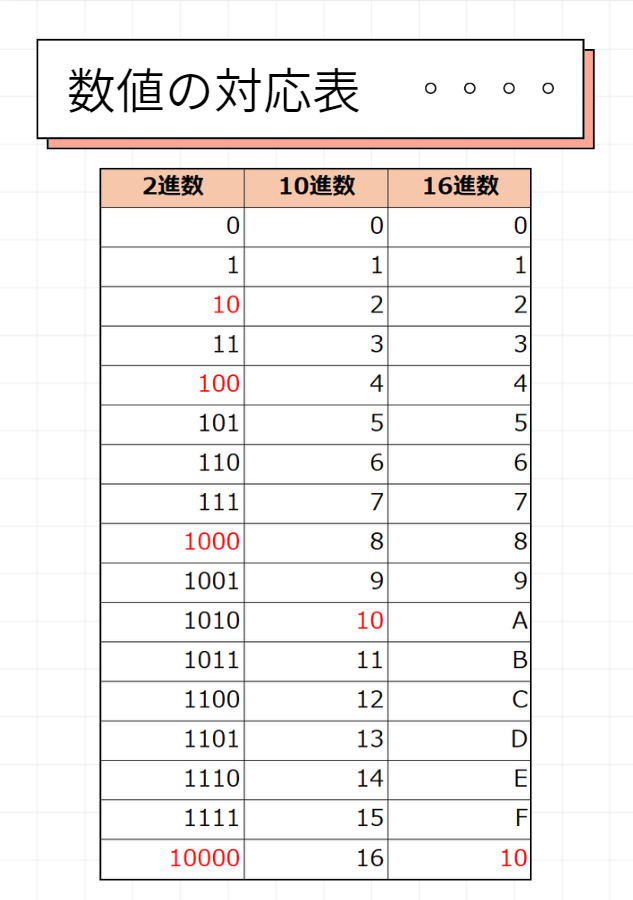
数値の対応表は頭に入れておくと便利なので、ぜひ参考にしてください！

基数について
基数とは、数値を表すときに「桁が上がる基準となる数」を指します。
例えば、10進数の基数は「10」、2進数の基数は「2」、16進数の基数は「16」です。
基数が変わると、使用できる数字の範囲や桁の意味が異なります。

そして、上の数値の対応表のように相互に変換することが可能です。
この変換のことを「基数変換」といいます。

基数変換

いよいよ、「基数変換」の解説をしていきます。
数値の対応表にある数値であれば簡単に基数変換を行うことができますが、それ以外は計算が必要となります。
最後には、練習問題も用意しているので、そちらも活用して慣れていきましょう！

2進数→10進数、10進数→2進数

では早速、「2進数⇆10進数」について解説していきます。

2進数→10進数
2進数を10進数に変換するためには、次の2つの手順が必要です。
1. 各桁に2進数の重みをかける
2. 各桁を足し合わせる
…と言われても、初めての場合は難しいですよね。そこで、より詳しく解説していきます。

「重み」とは、各桁の値を示す数です。
2進数の場合、桁が左に進むごとに重みは2の累乗で増えていきます。
具体的には次のようになります。
・（1の位）：2⁰=1
・（2の位）：2¹＝2
・（4の位）：2²=4
・（8の位）：2³=8

これを普段使用している10進数に当てはめると、
「10⁰=1, 10¹=10, 10²=100, 10³=1000, …」という形で桁が上がっていき、
各桁の位を表しています。
たとえば、(123)₁₀を考えると、次のような計算になります。
（括弧の右下に〇進数の〇を記入することで、数字が〇進数なのかを表すことができます。）
(1×10²)+(2×10¹)+(3×10⁰)=123

例として、2進数「1101」に当てはめてみましょう。各桁の重みと値を考えます。
・（1の位）：1×2⁰=1
・（2の位）：0×2¹=0
・（4の位）：1×2²=4
・（8の位）：1×2³=8
それらを足し合わせると、
「8+4+0+1=13」となり、2進数「1101」は10進数の「13」と分かります。

10進数→2進数
次に、10進数を2進数に変換するためには、次の2つの手順が必要です。
1.商が0になるまで2で割り続ける
2.余りを下から上に並べる

では早速、先ほど得た(13)₁₀を例に交えて説明していきます。
まずは、(13)₁₀を商が0になるまで2で割り続けます。
・1回目：13÷2＝6…1
・2回目：6÷2＝3…0
・3回目：3÷2＝1…1
・4回目：1÷2＝0…1
ここで商が0になったため、あとは余りを下から上に並べると「1101」となり、
2進数への変換ができました。

これももちろん10進数に当てはまります。
たとえば、(123)₁₀を考えると、次のようになります。
・1回目：123÷10＝12…3
・2回目：12÷10＝1…2
・3回目：1÷10＝0…1
余りを下から上に並べると「123」となり、元の数が得られました。

10進数→16進数、16進数→10進数

では次に、「10進数⇆16進数」について解説していきます。

10進数→16進数
10進数を16進数に変換するためには、次の2つの手順が必要です。
1.商が0になるまで16で割り続ける
2.余りを下から上に並べる
割る数が変わるだけでやり方は10進数→2進数と変わりません。

では早速、(123)₁₀を例に交えて説明していきます。
まずは、(123)₁₀を商が0になるまで16で割り続けます。
・1回目：123÷16＝7…11
・2回目：7÷16＝0…7
ここで商が0になったため、あとは余りを下から上に並べていきます。
10進数の「7」は16進数でも「7」のためそのまま、
10進数の「11」は16進数では「B」となります。
このことから、(123)₁₀は(7B)₁₆であることが分かり、変換することができました。

10～15の数は、A～Fのアルファベットに置き換える必要があることを覚えておきましょう！

16進数→10進数
次に、16進数を10進数に変換するためには、次の2つの手順が必要です。
1. 各桁の16進数を10進数に置き換える
2. 各桁に16進数の重みをかけ、各桁を足し合わせる
かける数が16進数の重みが変わるだけでやり方は2進数→10進数と変わりませんが、
その前に各桁の16進数を10進数に置き換える必要があります。

例として(7B)₁₆を例に交えて説明していきます。
最初に、各桁の16進数を10進数に置き換えます。
・(7)₁₆→(7)₁₀
・(B)₁₆→(11)₁₀

次に、各桁に16進数の重みをかけ、足し合わせます。
・（1の位）：11×16⁰=11
・（16の位）：7×16¹=112
それらを足し合わせると、
「11+112=123」となり、16進数「7B」は10進数の「123」と分かります。

このように、基数に応じて数を変えれば、さまざまな進数での表現が可能になります。

練習問題

練習問題を5問用意しましたので、挑戦してみてください！
解説も用意しているので解き終わったら、確認してください。

解説

問1 2進数「100011」を10進数に変換したものはどれか。
2進数から10進数に変換するためには、各桁に2進数の重みをかけ、足し合わせます。
・（1の位）：1×2⁰=1
・（2の位）：1×2¹=2
・（4の位）：0×2²=0
・（8の位）：0×2³=0
・（16の位）：0×2⁴=0
・（32の位）：1×2⁵=32
それらを足し合わせると、
「32+0+0+0+2+1＝35」となり、2進数「100011」は10進数の「15」と分かります。

問2 10進数「62」を2進数に変換したものはどれか。
10進数から2進数に変換するためには、商が0になるまで2で割り続けて、余りを下から上に並べます。
・1回目：62÷2＝31…0
・2回目：31÷2＝15…1
・3回目：15÷2＝7…1
・4回目：7÷2＝3…1
・5回目：3÷2＝1…1
・6回目：1÷2＝0…1
ここで商が0になったため、あとは余りを下から上に並べると、
10進数「62」は2進数の「111110」と分かります。

問3 10進数「138」を16進数に変換したものはどれか。
10進数から16進数に変換するためには、商が0になるまで16で割り続けて、余りを下から上に並べます。
・1回目：138÷16＝8…10
・2回目：8÷16＝0…8
ここで商が0になったため、あとは余りを下から上に並べると、
10進数「138」は16進数の「8A」と分かります。
※10～15の数は、A～Fのアルファベットに置き換えるのを忘れずに！

問4 16進数「1DA」を10進数に変換したものはどれか。
16進数から10進数に変換するためには、各桁の16進数を10進数に置き換えたあと、各桁に16進数の重みをかけ、足し合わせます。
最初に、各桁の16進数を10進数に置き換えます。
・(1)₁₆→(1)₁₀
・(D)₁₆→(13)₁₀
・(A)₁₆→(10)₁₀
次に、各桁に16進数の重みをかけ、足し合わせます。
・（1の位）：10×16⁰=10
・（16の位）：13×16¹=208
・（16の位）：1×16²=256
それらを足し合わせると、
「256+208+10＝474」となり、16進数「1DA」は10進数の「474」と分かります。

問5 【チャレンジ】16進数「2A」を2進数に変換したものはどれか。
16進数を2進数に変換するためには、2つの方法があります。
1つ目は10進数を経由する方法、2つ目は直接変換する方法です。

方法1：10進数を経由する方法
※それぞれの基数変換の説明は省略しています。
まずは、16進数「2A」を10進数に変換します。
・16進数「2A」→10進数「42」
次に、10進数「42」を2進数に変換します。
・10進数「42」→2進数「101010」
これで、16進数「2A」は2進数の「101010」であると分かります。

方法2：直接変換する方法
まずは、16進数の各桁を個別に2進数に変換します。
・(2)₁₆→(0010)₂　
・(A)₁₆→(1010)₂　
次に、その2進数を並べます。その際、前にある余分な0は消して大丈夫です。
・(2A)₁₆→(101010)₂
これで、16進数「2A」は2進数の「101010」であると分かります。

これと反対に2進数から16進数に変換する際は、
1.右端から4ビットずつ区切る
2.各4ビットを16進数に変換する
この手順で直接変換することができます。
例：(101010)₂→0010 1010→(2A)₁₆
※4ビットに満たない場合は左側にゼロを補います。

直接変換する方法はITパスポート試験に合格するために必須ではないため、無理に覚える必要はありません。
まずは10進数を経由する考え方を覚えておきましょう！